Critical Distance and Acoustics

What is Critical Distance ?

In sound reproduction, achieving a balanced listening experience depends on the interaction between the direct sound from the speakers and the reflected sound bouncing around the room (often referred to as the diffuse field).

This ideal balance is often described as a 50/50 ratio of direct to reverberated sound. However, this is a guideline, and preferences can vary depending on the music and your personal taste, with some favoring a 60/40 or 40/60 mix.

The critical distance is the distance from the speakers where the direct and reflected sound levels become roughly equal. It’s influenced by two key factors:

• Room Acoustics (Sabine Absorption): Rooms with lower absorption (more reflective surfaces) tend to have a longer critical distance. This is because sound reflects more readily, maintaining a higher level of reverberated sound even at further distances. Conversely, rooms with higher absorption (more sound-absorbing materials) have a shorter critical distance as the sound gets dampened more quickly, reducing the level of reflected sound.

• Speaker Directivity Factor: Speakers with a wider dispersion pattern (spreading sound over a larger area) generally have a shorter critical distance when a narrower ones has a longer one. This is because the off-axis sound increasing sound energy by bouncing off walls and other surfaces.

  • Wider Dispersion: Speakers with a wider dispersion pattern (spreading sound over a larger area) generally have a shorter critical distance. This is because they excite a larger portion of the room with off-axis direct sound, leading to a higher overall level of sound energy reaching the listener even at closer distances. However, these speakers also tend to contribute more to the reverberated field due to the increased sound energy bouncing off walls and other surfaces.
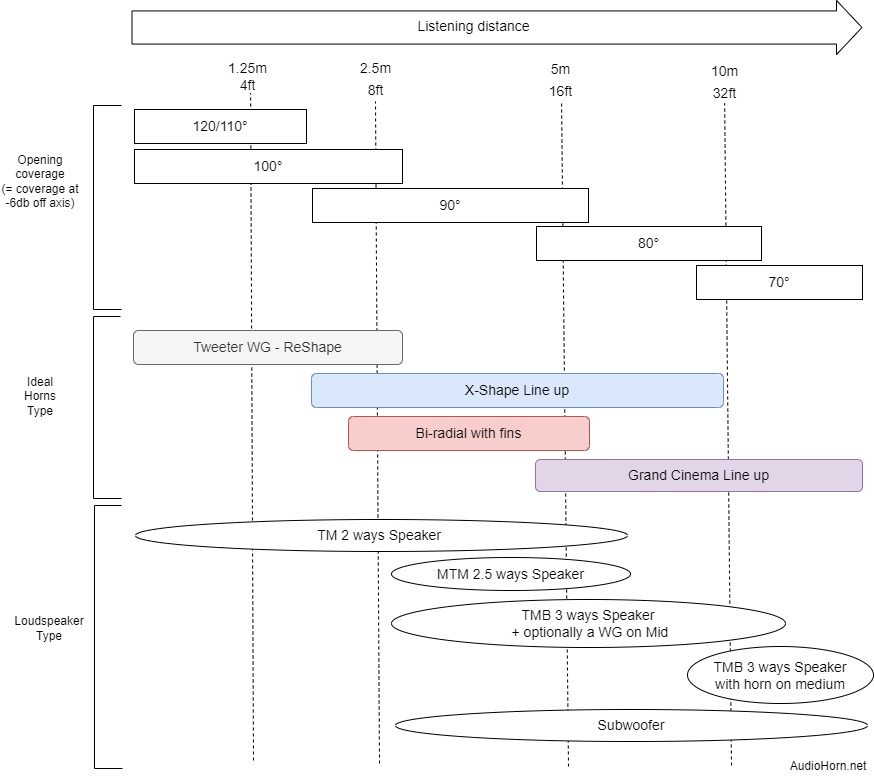
    Generally 90° constant directivity horn are adapted from 2/2m50 to 5/6m.

  • Narrower Dispersion: In contrast, speakers with a narrower dispersion pattern focus sound energy within a more concentrated cone. This means that a smaller portion of the room is directly excited, requiring a longer listening distance to achieve a similar level of sound energy compared to wider dispersion speakers. While they contribute less to the overall reverberated sound due to the focused sound direction, achieving a balanced sound experience with these speakers might necessitate sitting further away.
    Generally 80/70° constant directivity horn are used after 5/6m.

Additional Considerations:

• Frequency and Directivity: The balance between direct and reverberated sound can also vary with frequency due to speaker directivity. Speakers with constant directivity help to maintain a more consistent balance across the listening area.

• Speaker Placement: While not directly related to critical distance, proper speaker placement can enhance the sound experience. Avoid placing the listening position (sofa) directly against the wall. This ensures the listener isn’t too close to the wall, affecting the ideal balance of direct and reflected sound. Additionally, maintaining some space between the seating area and the walls promotes better sound dispersion throughout the room. Angling the speakers slightly towards the listening area can create a more focused and engaging soundstage.

The formula can be found in Appendix A.

Why Respect It?

Respecting critical distance, along with using constant directivity devices and proper acoustic treatment when possible, allows us to achieve an optimal sound balance in the listening room. This translates to several benefits:

More Neutral and Faithful Sound: By achieving a balanced mix of direct and reflected sound, we hear the audio closer to how it was intended to be heard by the artist or sound engineer. The sound becomes more natural and accurate, avoiding unwanted coloration.

Increased Listening Volume Without Fatigue: Our hearing is generally more sensitive and find their limit at the most sensitive part of our ears. When the critical distance is not respected, especially in rooms with low absorption, reflections can cause an excess of high-frequency energy. This creates a fatiguing and harsh sound, forcing us to listen at lower volumes.

By adapting directivity to our listening distance, we can achieve two key benefits:

• Controlled High Frequencies: The speaker’s directivity helps focus high-frequency sound towards the listener, reducing uncontrolled reflections and preventing high frequencies from becoming harsh or fatiguing. This targeted approach allows for a more balanced energy spectrum across all frequencies. The highs won’t overpower the lows, resulting in a more natural,faithful and detailed listening experience.

• Improved Lower Frequency Presence and higher volume listening: With a balanced energy spectrum, we can listen at higher volumes without experiencing ear fatigue caused by excessive high frequencies, critical distance plays a role in how we perceive the low frequencies in comparaison to the high ones when they are controlled according to listening distance and with constant directivity behavior.
  When the balance is right, the low frequencies will have a stronger presence without overpowering the rest of the sound.

In simpler terms, respecting critical distance helps us achieve a more natural, balanced, and enjoyable listening experience at higher volumes without listener fatigue.

Modern Speaker Design: Beyond the 120-Degree Coverage Myth

Nowadays, many loudspeakers prioritize achieving a strict 120-degree sound dispersion (directivity) across all frequencies.

However, this “one-120°-coverage-fits-all” approach ignores psychoacoustics (how we hear) and the great impact of listening distance.

In most rooms, a 90-degree horizontal constant directivity provides a more even distribution of sound energy, creating a well-balanced listening experience.

This approach recognizes the concept of critical distance. Conversely, 120 degree dispersion in a typical listening environment will excite sidewalls too many (creating too much reflected sound) and will make the sound less and less balanced and more and more aggressive the further we go away to the speakers.

Here is a guide for listening distance and type of horn with coverage (most of our horns are availables in several coverage) we can use:

Direct, Diffuse Field and Modal regime

Understanding the behavior of sound waves in a room is crucial for achieving a good listening experience. Here, we’ll differentiate between two key concepts and explore some additional factors influencing low-frequency response:

Direct and Diffuse Field

• Direct Field: This refers to the sound that travels directly from the source (speakers) to the listener without any reflections from walls or other surfaces. The intensity of the direct field decreases with distance following the inverse square law, meaning it weakens by 6 dB for each doubling of distance. This is why sound gets progressively quieter as you move further away from the speakers.

• Diffuse Field: A diffuse sound field is one that is homogeneous and isotropic (exhibits the same properties in all directions) throughout the volume of a room at any given time. It is made up of an infinite number of plane waves propagating in all directions. There are no major room-related anomalies to be observed in the measurements. Unlike the direct field, the diffuse field level is considered relatively constant within the listening area. This is because the sound has reflected numerous times and reached the listener from various directions, averaging out any distance-related variations.

It’s important to note: While the diffuse field is considered relatively constant within the listening zone, the overall sound pressure level (SPL) in a room, including the contribution from the diffuse field, will still decrease with distance from the speakers following the inverse square law. This decrease is primarily caused by the direct sound attenuating with distance, while the diffuse field level remains more stable within the listening area.

Modal Regime and Modes:

In addition to the concepts above, two other factors significantly influence how sound behaves in a room, particularly at lower frequencies:

• Modal Regime: This refers to a situation where reflections are very important but localized and resonate at specific frequencies. These localized reflections coexist with absorptions at nearby frequencies, leading to a chaotic response, especially noticeable in the low frequencies (30-80Hz) of typical living rooms.

• Modes: These chaotic responses manifest as large peaks and dips (typically +/- 15dB) in the sound pressure level at specific frequencies. They arise because the room dimensions create resonances where sound waves are reflected back and forth, reinforcing certain frequencies and cancelling others.

The consequence of these modes is the creation of resonance frequencies and a type of reverberation that’s specific to the room itself. Even small changes in speaker position can significantly alter this response.

Schroeder Frequency:

The Schroeder frequency is a critical transition zone, often with a wide range, that separates the modal regime from the diffuse field. Below the Schroeder frequency, the modal regime dominates, leading to the chaotic response described earlier. Above the Schroeder frequency, the diffuse field becomes more prominent, with sound reflecting more randomly throughout the room and creating a smoother response.

Room Size and Schroeder Frequency: The size of the room significantly impacts the Schroeder frequency. Larger rooms have a lower Schroeder frequency. In very large rooms, the Schroeder frequency can even fall outside the audible range of human hearing. This means that even low frequencies will exhibit a more diffuse character, which is often considered ideal for listening experiences. In these large rooms, the density of modes in the low frequencies becomes high enough to create a diffuse response.

The formula can be found in Appendix B.

Time Period of Integration (TPI), the brain interpretation:

The time period of integration (TPI) is the time window within which our auditory system perceives sound reflections as part of the direct sound rather than distinct echoes. This phenomenon is known as the “fusion effect.”

• If a reflection (Diffuse Field) arrives within a certain time delay (TPI), it merges with the direct sound, creating a single auditory event.
• If the delay exceeds the TPI, the reflection is perceived as a separate echo.

The TPI depends on several factors:

• Frequency: TPI is generally longer at lower frequencies and shorter at higher frequencies.
• Distance: The TPI increases with the distance between the sound source and the listener.
• Head size: The TPI is slightly affected by the size of the listener’s head.

Additional Factors:

The TPI is influenced by various factors beyond the distance and frequency:

• Sound type: Complex sounds like speech have longer TPIs than pure tones.
• Listening environment: TPI can be longer in noisy environments.
• Listener’s age: TPI tends to increase with age.
• Level difference between direct sound and reflections: Higher level differences lead to shorter TPIs.

Thévenot’s Fusion Curve:

This curve illustrates the relationship between the TPI and the level difference between the direct sound and its reflection.
A higher level difference allows for a longer TPI, meaning that reflections can arrive later without being perceived as echoes.

The formula can be found in Appendix C.

Haas Effect

The Haas effect is a psychoacoustic phenomenon related to the TPI.

If two identical sounds arrive very close together (under 35 milliseconds), our brains perceive them as a single sound coming from the direction of the first sound to arrive.

This allows sound engineers to increase sound level in the back of a room without affecting perceived sound direction by using delaying signal sent to a relay speaker.

In room accoustics in our reverberated field the early reflection on the near wall can create another “virtual” source and enter in Haas effect, it can be negative if the amplitude of this virtual source is too high.

Conclusion and additional considerations:

The critical distance formula is most accurate in ideal conditions with a well-established diffuse sound field (even distribution of sound throughout the room). In real rooms, this might not always be the case.

The formula is also only strictly valid if the listening position is directly on the speaker axis.

There’s no one-size-fits-all solution. Experiment, consider the factors mentioned, and personalize your listening experience, there is no golden rule because every room acoustics is different, but we often see:

• 90° constant directivity horn: 2/2m50 to 5/6m
• 80/70° constant directivity horn: 5/6m and more
• Line array: very long distance outdoors (large festivals, no obstavle), the distance between the center of the first speaker and the center of the last speaker must be equal to or greater than the wavelength of the lowest frequency reproduced, knowing that 80hz is a wavelength of 4m25.
  The main goal of line array is in fact to maintain SPL for everybody at distance, nor really the directivity.

Appendix A: Calculating Your Ideal Listening Distance

Experiment with different listening distances to find the sweet spot that sounds best to you.
Consider the size of your room and the type of speakers you have.
Take into account your personal preferences for a more direct or spacious sound.

Critical Distance Formula:

The critical distance, which is the theoretical distance for achieving a 50/50 balance, can be calculated using the following formula:

dc = √(αQ / 50)

Where:

dc is the critical distance in meters
α is the Sabine absorption equivalent in m²/s (explained below)
Q is the directivity factor of the speaker (a value representing how the speaker spreads sound)

Directivity factor represents the speaker’s tendency to focus sound in specific directions compared to an ideal omnidirectional source radiating sound equally in all directions.

High Q: Indicates a more directional speaker, concentrating sound energy in a narrower beam.
Low Q: Indicates a more omnidirectional speaker, radiating sound more evenly.

Understanding Q is crucial in the formula as it influences the critical distance (dc):

Higher Q (more directional): Leads to a greater critical distance. This means you can sit further away from the speaker and still maintain a good balance between direct and reflected sound (50/50 ratio).
Lower Q (less directional): Results in a shorter critical distance. You need to sit closer to the speaker to achieve the desired balance.

Remember:

• Q is usually measured in decibels (dB).

• It often varies with frequency.

• Speaker design significantly impacts directivity.

Sabine Absorption Equivalent (α):

The Sabine absorption equivalent (α) represents the total sound-absorbing capacity of a room. It essentially measures how effectively a room absorbs sound energy and prevents reflections. A higher α value indicates greater sound absorption, leading to a shorter reverberation time (less echo) and a potentially quieter environment. Conversely, a lower α value means more reflections and a longer reverberation time, resulting in a noisier and potentially less comfortable space.

Calculating Sabine Absorption:

The total Sabine absorption of a room can be calculated by summing the product of the surface area of each material and its corresponding sound absorption coefficient (SAC).

Total Absorption (α) = Σ (Surface Area x Sound Absorption Coefficient)

Σ (sigma) represents the summation over all materials in the room.

Sound Absorption Coefficient (SAC):

The sound absorption coefficient (SAC) is a value between 0 (perfectly reflective) and 1 (perfectly absorbent) that specifies how well a particular material absorbs sound at different frequencies. Different materials have different SAC values, and understanding these values is crucial for calculating the total Sabine absorption of a room.

Appendix B: Schroeder frequency formula

Fs = 2000 * √(T/V)

Where:

Fs is the Schroeder frequency in Hertz (Hz)
T is the reverberation time of the room in seconds (s)
V is the volume of the room in cubic meters (m³)

Appendix C: TPI formula

The TPI can be estimated using various formulas, including:

Schroeder’s Formula: TPI = 0.6 * (c / f) * (1 + (d / r))
Blauert’s Formula: TPI = 1.5 * (c / f) * (1 + (d / r))^0.5
Houtgast’s Formula: TPI = 4.2 * (c / f) * (1 + (d / r))^0.4

Where:

c is the speed of sound (approximately 343 m/s)
f is the sound frequency in Hertz (Hz)
d is the distance between the sound source and the listener (in meters)
r is the radius of the listener’s head (approximately 0.0875 m)